Introductory Statistics
This comprehensive course, combined with the easy-to-use teaching and learning tools in Odigia’s leading learner engagement platform, has everything you need to track, assess, engage, and collaborate with your students. This course comes with content and pre-built assessment questions which can be easily customized or used as-is. Our advanced math editor includes the ability for dynamic and unique variations of questions, as well as the option to customize or create additional practice, quiz, or test questions.
This course includes:

575
dynamic, multi-version questions

23
engagement activities
Helping Teachers Do What They Do Best: Teach

Customize
Use our courses as is or easily customize them to fit your teaching style and the needs of your students. You can add your favorite resources, hide and show our existing content and pre-built assessments, or make them your own. Everything your students need, in one place!

Engage and Collaborate
Odigia combines learning materials, discussions, and tools to create a familiar social experience for students allowing you to easily connect and redirect students attention.

Track
See how much time students are spending on different areas of the course, which areas are creating the most amount of engagement and identify topics the students are struggling with. Flag and provide feedback on assignments to proactively meet individual students' needs.

Assess
Game theory allows students to monitor their progress visually and motivates them to stay on track. Students can see exactly what activities they need to complete, which ones have been flagged and compare their progress against the overall class.
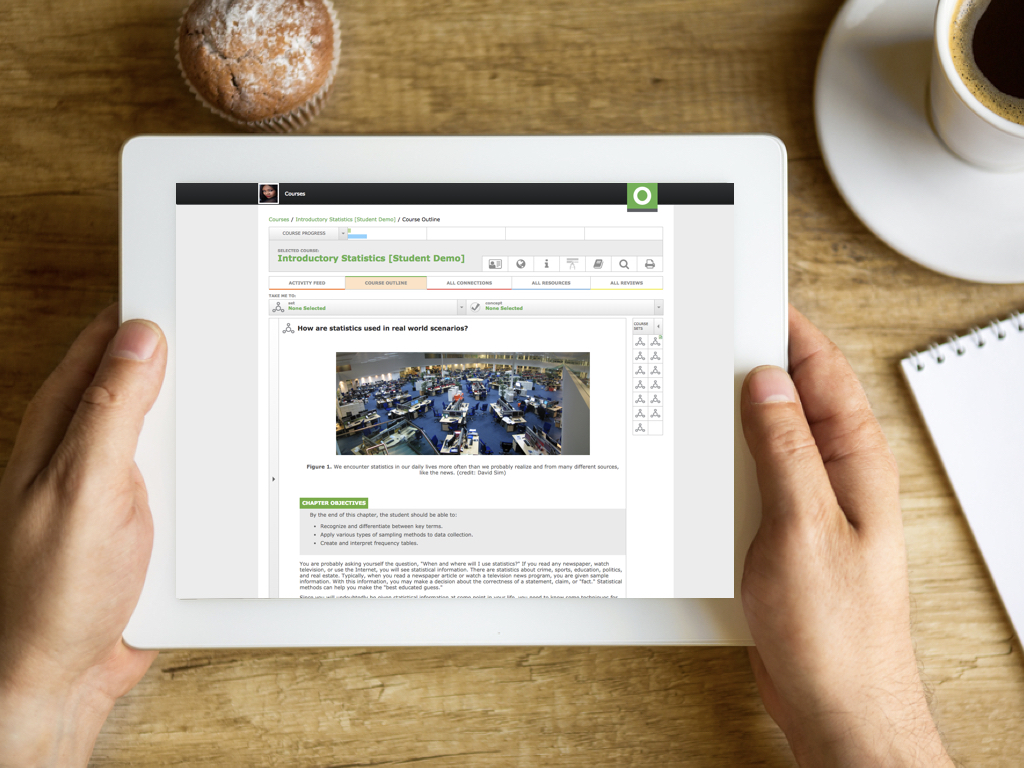
Introductory Statistics Course Outline
How are statistics used in real world scenarios?
- How are statistics and probability defined?
- How do you design an ethical experiment?
- What are the different types of data and sampling?
- How do you organize data?
- Data Collection Experiment
- Sampling Experiment
What is Descriptive Statistics?
- What are some tools of Descriptive Statistics?
- How else can you display data?
- How do you measure location?
- How do you display location?
- What is the “center” of a set?
- How do you describe distribution?
- How do you describe spread of data?
- Descriptive Statistics Activity
What is Probability?
- What are important probability terms?
- How are events related?
- What are some tools of Probability?
- What is a Contingency Table?
- How do you deal with complex probability problems?
- Probability Exercise
What is a Discrete Random Variable?
- What is a Probability Distribution Function?
- How do you estimate an Expected Value?
- What is a Binomial Distribution?
- What is a Geometric Distribution?
- What is a Hypergeometric Distribution?
- What is a Poisson Distribution?
- Discrete Distribution (Playing Card Experiment)
- Discrete Distribution (Lucky Dice Experiment)
What is a Continuous Random Variable?
- How do you estimate Probability in Continuous Probability Functions?
- What is a Uniform Distribution?
- How can we estimate when an event will occur?
- Continuous Distribution Example
What does it mean to be 'normal'?
- What does “Standardized Normal Distribution” mean?
- How do you use a Normal Distribution?
- Normal Distribution Example (Lap Times)
- Normal Distribution Example (Pinkie Length)
Why are we concerned with 'means'?
- What is The Central Limit Theorem for sample means?
- What is The Central Limit Theorem for sums?
- How does one use the Central Limit Theorem?
- Central Limit Theorem Example (Pocket Change)
- Central Limit Theorem Example (Cookie Recipes)
How do you measure confidence?
- How do you analyze a single population mean using normal distribution?
- How do you analyze a single population mean using the Student t Distribution?
- How do you measure confidence for a Population?
- Confidence Interval Example (Home Costs)
- Confidence Interval Example (Place of Birth)
- Confidence Interval Example (Women’s Heights)
How do we test a hypothesis with one sample?
- What are the two types of hypotheses?
- What are the outcomes of a hypothesis test?
- What distribution is needed for hypothesis testing?
- What factors should you consider during a hypothesis test?
- Additional Information and Full Hypothesis Test Examples
- Hypothesis Testing of a Single Mean and Single Proportion Example
How do we test a hypothesis with two samples?
- How do you perform a hypothesis test with unknown standard deviations?
- How do you perform a hypothesis test with known standard deviations?
- How do you compare two independent population proportions?
- What do you do when you have matched or paired samples?
- Hypothesis Testing for Two Means and Two Proportions Example
How do we test the relationship between things?
- What is the Chi-Square Distribution?
- How well does the data “fit”?
- How do you test whether two sets are independent?
- How do you test whether two populations have the same distribution?
- Which Chi-Square Tests should you use?
- How do you perform a test of a single variance?
- Chi-Square Goodness-of-Fit Example
- Chi-Square Test of Independence Example
How do we test if events are correlated?
- What is a linear equation?
- How do you illustrate a relationship?
- What is a Regression Equation?
- How do you test the significance of the correlation coefficient?
- How do we make predictions?
- What is an outlier?
- Regression Example (Distance from School)
- Regression Example (Textbook Cost)
- Regression Example (Fuel Efficiency)
How do we compare averages of more than two groups?
- What is a ANOVA test?
- What is the F Distribution?
- What characterizes the F Distribution?
- What else can you use the F Distribution for?
- One-Way ANOVA Example
Introductory Statistics follows scope and sequence requirements of a one-semester introduction to statistics course and is geared toward students majoring in fields other than math or engineering. The text assumes some knowledge of intermediate algebra and focuses on statistics application over theory. Introductory Statistics includes innovative practical applications that make the text relevant and accessible, as well as collaborative exercises, technology integration problems, and statistics labs.ams.
About the authors:
Senior Contributing Authors
Barbara Illowsky, De Anza College
Susan Dean, De Anza College
Contributing Authors
Laurel Chiappetta, University of Pittsburgh
Lenore Desilets, De Anza College
Lisa Markus, De Anza College
Bryan Blount, Kentucky Wesleyan College
Carol Olmstead, De Anza College
Carol Weideman, St. Petersburg College
Charles Ashbacher, Upper Iowa University, Cedar Rapids
Charles Klein, De Anza College
Cheryl Wartman, University of Prince Edward Island
David French, Tidewater Community College
Dennis Walsh, Middle Tennessee State University
Diane Mathios, De Anza College
Ernest Bonat, Portland Community College
Jing Chang, College of Saint Mary
John Thomas, College of Lake County
Kathy Plum, De Anza College
Abdulhamid Sukar, Cameron University
Abraham Biggs, Broward Community College
Adam Pennell, Greensboro College
Alexander Kolovos
Andrew Wiesner, Pennsylvania State University
Ann Flanigan, Kapiolani Community College
Robert McDevitt, Germanna Community College
Roberta Bloom, De Anza College
Rupinder Sekhon, De Anza College
Sara Lenhart, Christopher Newport University
Sarah Boslaugh, Kennesaw State University
Sheldon Lee, Viterbo University
Sheri Boyd, Rollins College
Sudipta Roy, Kankakee Community College
Cindy Moss, Skyline College
Jonathan Oaks, Macomb Community College
Larry Green, Lake Tahoe Community College
Birgit Aquilonius, West Valley College
Jim Lucas, De Anza College
Mary Teegarden, San Diego Mesa College
Matthew Einsohn, Prescott College
Mel Jacobsen, Snow College
Michael Greenwich, College of Southern Nevada
Miriam Masullo, SUNY Purchase
Mo Geraghty, De Anza College
Nydia Nelson, St. Petersburg College
Philip J. Verrecchia, York College of Pennsylvania
Robert Henderson, Stephen F. Austin State University
Benjamin Ngwudike, Jackson State University
Daniel Birmajer, Nazareth College
David Bosworth, Hutchinson Community College
Frank Snow, De Anza College
George Bratton, University of Central Arkansas
Inna Grushko, De Anza College
Janice Hector, De Anza College
Javier Rueda, De Anza College
Jeffery Taub, Maine Maritime Academy
Jim Helmreich, Marist College
Lisa Rosenberg, Elon University
Lynette Kenyon, Collin County Community College
Mark Mills, Central College
Mary Jo Kane, De Anza College
Travis Short, St. Petersburg College
Valier Hauber, De Anza College
Vladimir Logvenenko, De Anza College
Wendy Lightheart, Lane Community College
Yvonne Sandoval, Pima Community College
Assessment Question Author
William C. Fanning
Adjunct Mathematics Professor
Central Virginia Community College

