Calculus Volume 2
The comprehensive contents from this book, combined with Odigia’s Teaching and Learning Tools have everything you need to engage, collaborate, track and assess your students.

See How Odigia Works

This course includes:

235

example problems

315

practice questions

Helping Teachers Do What They Do Best: Teach

Customize

Use our courses as is or easily customize them to fit your teaching style and the needs of your students. You can add your favorite resources, hide and show our existing content and pre-built assessments, or make them your own. Everything your students need, in one place!

Engage and Collaborate

Odigia combines learning materials, discussions, and tools to create a familiar social experience for students allowing you to easily connect and redirect students attention.

Track

See how much time students are spending on different areas of the course, which areas are creating the most amount of engagement and identify topics the students are struggling with. Flag and provide feedback on assignments to proactively meet individual students' needs.

Assess

Game theory allows students to monitor their progress visually and motivates them to stay on track. Students can see exactly what activities they need to complete, which ones have been flagged and compare their progress against the overall class.

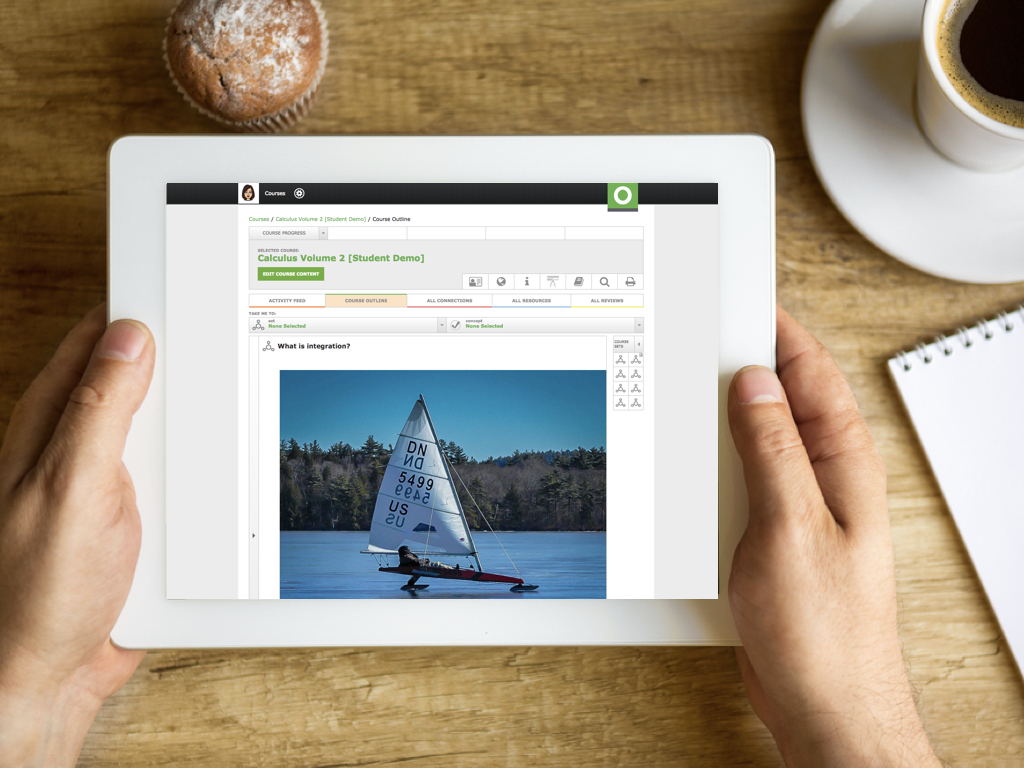
Calculus Volume 2 Course Outline

What is integration?

Concepts Covered:

  • How are areas approximated?
  • What is the definite integral?
  • What is the meaning of the Fundamental Theorem of Calculus?
  • How are integration formulas and the net change theorem applied?
  • How is substitution used to evaluate definite and indefinite integrals?
  • What are integrals involving exponential and logarithmic functions used for?
  • How are integrals resulting in inverse trigonometric functions integrated?

How is integration applied?

Concepts Covered:

  • How is the area between curves calculated?
  • How is volume determined by slicing?
  • What are volumes of revolution as related to cylindrical shells?
  • How are the arc length of a curve and surface area calculated?
  • What are physical applications in calculus?
  • How do centers of mass change under certain conditions and moments?
  • What is the relationship between integrals, exponential functions, and logarithms?
  • How is exponential growth and decay determined?
  • What are Hyperbolic Functions, and how are they solved?

Why is understanding the different techniques of integration important?

Concepts Covered:

  • When should the technique of integration by parts be used?
  • What are trigonometric integrals?
  • When should trigonometric substitution be used?
  • What are partial fractions?
  • What are some other strategies for integration?
  • How is numerical integration achieved?
  • How are improper integrals defined?

How are differential equations solved and used?

Concepts Covered:

  • What are the basics of differential equations?
  • How are differential equations solved with direction fields and numerical methods?
  • What are separable equations?
  • What is the logistic equation?
  • How are first-order linear equations solved?

How are sequences and series used in calculus?

Concepts Covered:

  • How are the formulas and limits of sequences found?
  • What are infinite series?
  • How are divergence and integral tests performed?
  • Why are comparison tests significant?
  • How are alternating series used and solved?
  • What are ratio and root tests?

What are power series?

Concepts Covered:

  • How are power series and functions identified?
  • What are the properties of power series?
  • What are Taylor and Maclaurin series?
  • How are Taylor Series used to solve different types of equations?

What is the significance of parametric equations and polar coordinates?

Concepts Covered:

  • How are parametric equations recognized?
  • What is the calculus of parametric curves?
  • What are polar coordinates?
  • How are the area and arc length in polar coordinates found?
  • How are conic sections evaluated?

About the book

Calculus Vol. 2

Calculus is designed for the typical two- or three-semester general calculus course, incorporating innovative features to enhance student learning. The book guides students through the core concepts of calculus and helps them understand how those concepts apply to their lives and the world around them. Due to the comprehensive nature of the material, we are offering the book in three volumes for flexibility and efficiency. Volume 2 covers integration, differential equations, sequences and series, and parametric equations and polar coordinates.

About the authors:

Senior Contributing Authors

Gilbert Strang, Massachusetts Institute of Technology
Edwin “Jed” Herman, University of Wisconsin-Stevens Point

Contributing Authors

William Radulovich, Formerly at Florida State College at Jacksonville
Erica M. Rutter, Arizona State University
David Smith, University of the Virgin Islands
Kirsten R. Messer, Colorado State University-Pueblo
Alfred K. Mulzet, Florida State College at Jacksonville
Nicoleta Virginia Bila, Fayetteville State University
Sheri J. Boyd, Rollins College
Joyati Debnath, Winona State University
Michelle Merriweather, Bronxville High School
Valeree Falduto, Palm Beach State College
Elaine A. Terry, Saint Joseph’s University
David Torain, Hampton University
Catherine Abbott, Keuka College
Joseph Lakey, New Mexico State University
Julie Levandosky, Framingham State University
David McCune, William Jewell College

 
Join other subject matter experts who are currently building courses in Odigia. 

Share knowledge and expertise while earning extra income.  

Learn More