Calculus Volume I
This comprehensive course, combined with the easy-to-use teaching and learning tools in Odigia’s leading learner engagement platform, has everything you need to track, assess, engage, and collaborate with your students. This course comes with content and pre-built assessment questions which can be easily customized or used as-is. Our advanced math editor includes the ability for dynamic and unique variations of questions, as well as the option to customize or create additional practice, quiz, or test questions.

See How Odigia Works

This course includes:

548

dynamic, multi-version questions

Helping Teachers Do What They Do Best: Teach

Customize

Use our courses as is or easily customize them to fit your teaching style and the needs of your students. You can add your favorite resources, hide and show our existing content and pre-built assessments, or make them your own. Everything your students need, in one place!

Engage and Collaborate

Odigia combines learning materials, discussions, and tools to create a familiar social experience for students allowing you to easily connect and redirect students attention.

Track

See how much time students are spending on different areas of the course, which areas are creating the most amount of engagement and identify topics the students are struggling with. Flag and provide feedback on assignments to proactively meet individual students' needs.

Assess

Game theory allows students to monitor their progress visually and motivates them to stay on track. Students can see exactly what activities they need to complete, which ones have been flagged and compare their progress against the overall class.

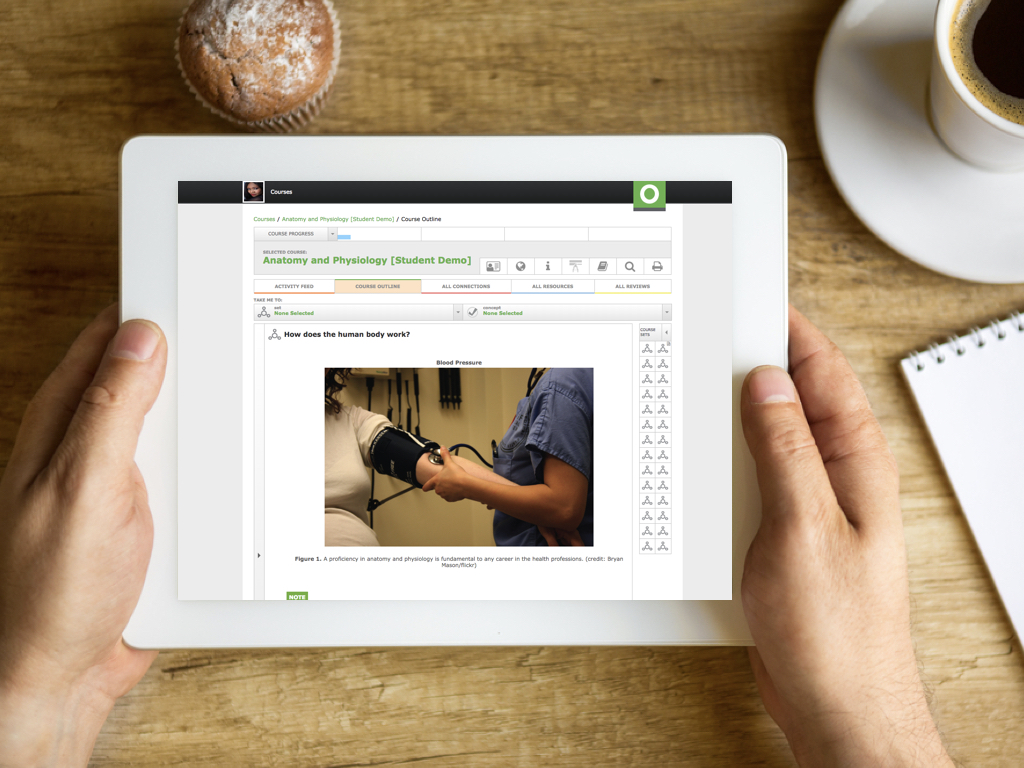
Calculus Volume I Course Outline

What functions are necessary to study calculus?

Concepts Covered:

What are the basic properties of functions?
What are the basic classes of functions?
How do trigonometric functions behave?
What are inverse functions?
What is the relationship between exponential and logarithmic functions?

Why are limits so important in calculus?

Concepts Covered:

How are limits used to solve problems in calculus?
How is the limit of a function determined?
What are the limit laws?
At what conditions is continuity achieved?
What is the precise definition of a limit?

How are derivatives calculated and used in calculus?

Concepts Covered:

How is the derivative defined?
How is the derivative of a function calculated?
What are the differentiation rules?
How are derivatives used as rates of change?
What are the derivatives of trigonometric functions?
How is the chain rule defined, and what is its function?
How are derivatives of inverse functions determined?
What is implicit differentiation?
How are derivatives of exponential and logarithmic functions found?

What are the different applications of Derivatives?

Concepts Covered:

How are related rates expressed in terms of derivatives?
How are linear approximations and differentials calculated?
What are maxima and minima?
What is the significance of the Mean Value Theorem
How do derivatives affect the shape of a graph?
What do limits at infinity and asymptotes look like?
How are applied optimization problems solved?
When should L’Hôpital’s Rule be applied?
What is Newton’s Method?
How are antiderivatives of functions found?

What is integration?

Concepts Covered:

How are areas approximated?
What is the definite integral?
What is the meaning of the Fundamental Theorem of Calculus?
How are integration formulas and the net change theorem applied?
How is substitution used to evaluate definite and indefinite integrals?
What are integrals involving exponential and logarithmic functions used for?
How are integrals resulting in inverse trigonometric functions integrated?

How is integration applied?

Concepts Covered:

How is the area between curves calculated?
How is volume determined by slicing?
What are volumes of revolution as related to cylindrical shells?
How are the arc length of a curve and surface area calculated?
What are physical applications in calculus?
How do centers of mass change under certain conditions and moments?
What is the relationship between integrals, exponential functions, and logarithms?
How is exponential growth and decay determined?
What are Hyperbolic Functions, and how are they solved?

About the book

Calculus Vol. 1

Calculus is designed for the typical two- or three-semester general calculus course, incorporating innovative features to enhance student learning. The book guides students through the core concepts of calculus and helps them understand how those concepts apply to their lives and the world around them. Due to the comprehensive nature of the material, we are offering the book in three volumes for flexibility and efficiency. Volume 1 covers functions, limits, derivatives, and integration.

About the authors:

Senior Contributing Authors

Gilbert Strang, Massachusetts Institute of Technology
Edwin “Jed” Herman, University of Wisconsin-Stevens Point

Contributing Authors

Alfred K. Mulzet, Florida State College at Jacksonville
Sheri J. Boyd, Rollins College
Joyati Debnath, Winona State University
Michelle Merriweather, Bronxville High School
Joseph Lakey, New Mexico State University
Elaine A. Terry, Saint Joseph’s University
David Smith, University of the Virgin Islands
Nicoleta Virginia Bila, Fayetteville State University
Valeree Falduto, Palm Beach State College
Kirsten R. Messer, Colorado State University-Pueblo
William Radulovich, Formerly at Florida State College at Jacksonville
Erica M. Rutter, Arizona State University
David Torain, Hampton University
Catherine Abbott, Keuka College
Julie Levandosky, Framingham State University
David McCune, William Jewell College

Assessment Question Author

William C. Fanning
Adjunct Mathematics Professor
Central Virginia Community College

Join other subject matter experts who are currently building courses in Odigia.

Share knowledge and expertise while earning extra income.

Learn More